Sponsored by Microsoft
Supported by Union Bank of
Switzerland
| Source file: Input file: |
stars.pas/stars.c/stars.C stars.in |
On a clear moon-less night, you can see millions of stars glimmering in the sky. Faced with this overwhelming number, the Greeks started nearly 2,000 years ago to bring some order to the chaos. They identified groups of stars, called constellations, and gave them names, mostly from the Greek mythology, that are still in use today. Examples are ``Ursa Minor'', ``Pisces'', ``Cancer'', and many others.
Given a sketch of the constellation, it is not easy for the amateur to actually find the constellation in the sky. Moreover, simple constellations, such as ``Triangulum'' (triangle,) which consists of only three stars, may appear several times in the sky. Again, singling out the ``correct'' occurrence is not easy.
Traditionally, maps were printed for just this purpose. But in this problem, we will see how the computer can help us find constellations in the sky.
You will be given a star map; for simplicity this will be a collection of points in the plane, each having a certain brightness associated with it. Then, given a constellation, also as a set of points in the plane, you are to determine:
An occurrence is a subset of stars from the map that forms a (possibly) arbitrarily rotated and/or scaled copy of the stars in the constellation.
The brightness of an occurrence is the average brightness of the stars it consists of, i.e. the sum of individual brightnesses divided by the number of stars in the constellation.
The input file contains the descriptions of several star maps. Each map starts with a line containing a single integer n, specifying the number of stars in the map (1 <= n < 1000). The following n lines contain three integers each, namely the x- and y-coordinates and the brightness of every star. The larger the value, the brighter the star shines.
The next line contains a single integer m, the number of constellations to follow (1 <= m < 50). Each constellation description starts with a line containing an integer si, the number of stars in constellation i, and a string Ni, the name of the constellation. (Ni will consist of no more than 40 characters and contain no blanks.) The following si lines then contain the coordinates of the constellation, again as x/y-pairs.
A blank line separates the star map from the next map. The input file ends with an empty map (having n = 0), which should not be processed.
N.B.: Since all star coordinates are integer numbers, you can easily rule out any rotated or scaled constellation whose points do not fall on integer coordinates.
For each star map first output the number of the map (`Map #1', `Map #2', etc.) on a line of its own.
For each constellation, in the same order as in the input, output first its name and how many times it occurs in the map on one line, as shown in the output sample.
If there is at least one occurrence, output the position of the brightest occurrence by listing the positions of the stars that form the brightest occurrence. The star positions have to be printed in ascending x-order. Positions having the same x-coordinates must be sorted in ascending y-order. If there are several equally bright solutions, output only one of them. Adhere to the format shown in the sample output.
Output a blank line before each constellation and a line of 5 dashes (`-----') after every star map.
6 1 2 1 2 1 4 2 4 3 3 2 1 4 1 5 4 3 2 2 3 Triangulum 1 1 3 1 2 4 4 Cancer 1 3 4 3 6 1 7 5 0
Map #1 Triangulum occurs 2 time(s) in the map. Brightest occurrence: (1,2) (4,1) (4,3) Cancer occurs 0 time(s) in the map. -----
[End of Problem A]
| Source file: Input file: |
hexagon.pas/hexagon.c/hexagon.C hexagon.in |
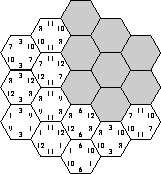
Consider a game board consisting of 19 hexagonal fields, as shown in the figure below. We can easily distinguish three main directions in the shape of the board: from top to bottom, from top-left to bottom-right, and from top-right to bottom-left. For each of these primary directions, the board can be viewed as a series of rows, consisting of 3, 4, 5, 4, and 3 fields, respectively.

The game board has to be completely covered using a set of hexagonal pieces. Each piece carries three numbers, one for every primary board direction. Only three different numbers are used for each direction. Every possible combination of three numbers for all three directions is assigned to a piece, leading to a set of 27 unique pieces. (The board in the above figure is still in the process of being covered.)
The score of a board is calculated as the sum of all 15 row scores (5 rows for each primary direction). The row scores are calculated as follows: if all pieces in a row carry the same number for the direction of the row, the row score is this number multiplied by the number of pieces in the row. Otherwise (the pieces carry different numbers in the row direction) the row score is zero. Note that the pieces may not be rotated. For example, the score of the leftmost row in the figure is 3 . 3 = 9, the score of the row to its right is 4 . 11 = 44.
While in the real game the pieces are chosen randomly and the set of pieces is fixed, we are interested in the highest possible score for a given set of numbers for each direction. This means you have to choose those 19 pieces that result in the highest score.
The first line of the input file contains an integer n which indicates the number of test cases. Each test case consists of three lines containing three integers each. Each of these three line contains the numbers for a single primary direction. From these numbers the set of pieces is generated.
For each test case output a line containing the number of the case (`Test #1', `Test #2', etc.), followed by a line containing the highest possible score for the given numbers. Add a blank line after each test case.
1 9 4 3 8 5 2 7 6 1
Test #1 308
[End of Problem B]
The following clarification was added to the problem during the last
minute announcements:
To simplify the problem, you should only consider
boards where each row has a score greater than zero, i.e. each piece in a row
carries the same number.
| Source file: Input file: |
domino.pas/domino.c/domino.C domino.in |
Did you know that you can use domino bones for other things besides playing Dominoes? Take a number of dominoes and build a row by standing them on end with only a small distance in between. If you do it right, you can tip the first domino and cause all others to fall down in succession (this is where the phrase ``domino effect'' comes from).
While this is somewhat pointless with only a few dominoes, some people went to the opposite extreme in the early Eighties. Using millions of dominoes of different colors and materials to fill whole halls with elaborate patterns of falling dominoes, they created (short-lived) pieces of art. In these constructions, usually not only one but several rows of dominoes were falling at the same time. As you can imagine, timing is an essential factor here.
It is now your task to write a program that, given such a system of rows formed by dominoes, computes when and where the last domino falls. The system consists of several ``key dominoes'' connected by rows of simple dominoes. When a key domino falls, all rows connected to the domino will also start falling (except for the ones that have already fallen). When the falling rows reach other key dominoes that have not fallen yet, these other key dominoes will fall as well and set off the rows connected to them. Domino rows may start collapsing at either end. It is even possible that a row is collapsing on both ends, in which case the last domino falling in that row is somewhere between its key dominoes. You can assume that rows fall at a uniform rate.
The input file contains descriptions of several domino systems. The first line of each description contains two integers: the number n of key dominoes (1 <= n < 500) and the number m of rows between them. The key dominoes are numbered from 1 to n. There is at most one row between any pair of key dominoes and the domino graph is connected, i.e. there is at least one way to get from a domino to any other domino by following a series of domino rows.
The following m lines each contain three integers a, b, and l, stating that there is a row between key dominoes a and b that takes l seconds to fall down from end to end.
Each system is started by tipping over key domino number 1.
The file ends with an empty system (with n = m = 0), which should not be processed.
For each case output a line stating the number of the case (`System #1', `System #2', etc.). Then output a line containing the time when the last domino falls, exact to one digit to the right of the decimal point, and the location of the last domino falling, which is either at a key domino or between two key dominoes. Adhere to the format shown in the output sample. If you find several solutions, output only one of them. Output a blank line after each system.
2 1 1 2 27 3 3 1 2 5 1 3 5 2 3 5 0 0
System #1 The last domino falls after 27.0 seconds, at key domino 2. System #2 The last domino falls after 7.5 seconds, between key dominoes 2 and 3.
[End of Problem C]
| Source file: Input file: |
pendulum.pas/pendulum.c/pendulum.C pendulum.in |
Consider a pendulum hanging on a string from a hook on a wall. When pushed, this pendulum will swing back and forth. Now imagine other hooks on the wall, placed in the path of our pendulum's string. The pendulum will bend around them, possibly even loop around them. In general, it will follow a much more complex path than before. After some time, the pendulum's motion will repeat, the pendulum will follow a periodic orbit. What we would like you to do is to compute the distance travelled by the pendulum as it completes one cycle of the orbit.
More formally, we place a cartesian coordinate system on the wall. The pendulum's string is affixed at the origin (0, 0). As usual, the x-axis points to the right and the y-axis points upwards. The string of the pendulum has a length of r. The pendulum is released at position (-r, 0) and therefore starts swinging to the right. Furthermore, there are n additional hooks distributed over the plane which may influence the path of the pendulum.
In our ideal world, the following assumptions are true:
Your program should simulate the movement of the pendulum and output the spatial length of the periodic orbit that it finally enters. As you may remember from physics: due to gravity, the pendulum will never reach a height greater than the one it started from! That is, it will never get above the x-axis. It will either reach its initial height again or circle endlessly around a hook in the wall.
The input file contains several test cases. Each case begins with a line containing an integer n (the number of hooks, 1 <= n < 500) and a real r (the length of the pendulum's string). The following n lines each contain two integers specifying the x- and y-coordinate of the corresponding hook.
The file ends with a case having r = 0, which should not be processed.
For each case output a line containing the number of the case (`Pendulum #1', `Pendulum #2', etc.).
Then print a line that contains the distance which the pendulum travels for completing one cycle of its periodic orbit. Do not count the distance travelled to reach the starting point of the orbit. (Adhere to the format shown in the output sample.) The distance should be exact to two digits to the right of the decimal point.
Output a blank line after each test case.
2 16.0 3 -4 -3 -4 1 18.0 5 -12 0 0
Pendulum #1 Length of periodic orbit = 87.66 Pendulum #2 Length of periodic orbit = 31.42
[End of Problem D]
| Source file: Input file: |
border.pas/border.c/border.C border.in |
You are to write a program that draws a border around a closed path into a bitmap, as displayed in the following figure:
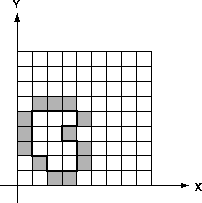
The path is closed and runs along the grid lines, i.e. between the squares of the grid. The path runs counter-clockwise, so if following the path is considered as going ``forward'', the border pixels are always to the ``right'' of the path. The bitmap always covers 32 by 32 squares and has its lower left corner at (0, 0). You can safely assume that the path never touches the bounding rectangle of the bitmap and never touches or crosses itself. Note that a bit gets set if it is on the outside of the area surrounded by the path and if at least one of its edges belongs to the path, but not if only one of its corners is in the path. (A look at the convex corners in the figure should clarify that statement.)
The first line of the input file contains the number of test cases in the file. Each test case that follows consists of two lines. The first line of each case contains two integer numbers x and y specifying the starting point of the path. The second line contains a string of variable length. Every letter in the string symbolizes a move of length one along the grid. Only the letters `W' (``west''), `E' (``east''), `N' (``north''), `S' (``south''), and `.' (``end of path'', no move) appear in the string. The end-of-path character ( `.') is immediately followed by the end of the line.
For each test case, output a line with the number of the case (`Bitmap #1', `Bitmap #2', etc.). For each row of the bitmap from top to bottom, print a line where you print a character for every bit in that row from left to right. Print an uppercase `X' for set bits and a period `.' for unset bits. Output a blank line after each bitmap.
1 2 1 EENNWNENWWWSSSES.
Bitmap #1
................................
<24
lines of periods
omitted>
................................
.XXX............................
X...X...........................
X..X............................
X...X...........................
.X..X...........................
..XX............................
[End of Problem E]
| Source file: Input file: |
villa.pas/villa.c/villa.C villa.in |
Mr. Black recently bought a villa in the countryside. Only one thing bothers him: although there are light switches in most rooms, the lights they control are often in other rooms than the switches themselves. While his estate agent saw this as a feature, Mr. Black has come to believe that the electricians were a bit absent-minded (to put it mildly) when they connected the switches to the outlets.
One night, Mr. Black came home late. While standing in the hallway, he noted that the lights in all other rooms were switched off. Unfortunately, Mr. Black was afraid of the dark, so he never dared to enter a room that had its lights out and would never switch off the lights of the room he was in.
After some thought, Mr. Black was able to use the incorrectly wired light switches to his advantage. He managed to get to his bedroom and to switch off all lights except for the one in the bedroom.
You are to write a program that, given a description of a villa, determines how to get from the hallway to the bedroom if only the hallway light is initially switched on. You may never enter a dark room, and after the last move, all lights except for the one in the bedroom must be switched off. If there are several paths to the bedroom, you have to find the one which uses the smallest number of steps, where ``move from one room to another'', ``switch on a light'' and ``switch off a light'' each count as one step.
The input file contains several villa descriptions. Each villa starts with a line containing three integers r, d, and s. r is the number of rooms in the villa, which will be at most 10. d is the number of doors/connections between the rooms and s is the number of light switches in the villa. The rooms are numbered from 1 to r; room number 1 is the hallway, room number r is the bedroom.
This line is followed by d lines containing two integers i and j each, specifying that room i is connected to room j by a door. Then follow s lines containing two integers k and l each, indicating that there is a light switch in room k that controls the light in room l.
A blank line separates the villa description from the next one. The input file ends with a villa having r = d = s = 0, which should not be processed.
For each villa, first output the number of the test case (`Villa #1', `Villa #2', etc.) in a line of its own.
If there is a solution to Mr. Black's problem, output the shortest possible sequence of steps that leads him to his bedroom and only leaves the bedroom light switched on. (Output only one shortest sequence if you find more than one.) Adhere to the output format shown in the sample below.
If there is no solution, output a line containing the statement `The problem cannot be solved.'
Output a blank line after each test case.
3 3 4 1 2 1 3 3 2 1 2 1 3 2 1 3 2 2 1 2 2 1 1 1 1 2 0 0 0
Villa #1 The problem can be solved in 6 steps: - Switch on light in room 2. - Switch on light in room 3. - Move to room 2. - Switch off light in room 1. - Move to room 3. - Switch off light in room 2. Villa #2 The problem cannot be solved.
[End of Problem F]
| Source file: Input file: |
ships.pas/ships.c/ships.C ships.in |
Probably everyone who ever attended school knows the game where two opposing players place a set of ships on a sheet of paper and try to eliminate each other's ships by guessing their location.
In our version of the game, your opponent has distributed the following seven ship patterns over a rectangular grid of squares:
xx xx xx
x x x
xx xx
xx xxx xxx xxx xxxx
Each ship pattern covers exactly four squares. The patterns may be rotated but not mirrored. All patterns are guaranteed to be placed completely within the boundaries of the rectangle and not to overlap each other, whereas touching another pattern or the border is allowed.
We assume that we are in the middle of the game and that several squares have already been uncovered. You will be given a rectangular grid of squares representing your current knowledge about the positions of your enemy's ships. Every square is marked by one of the following characters:
Given that information, you are to decide whether you can determine all remaining `x' squares with at most one miss, i.e. whether you could uncover the `.' squares without getting more than one `o' square before you had all `x' squares uncovered. This means you are allowed to hit a `o' if then the solution becomes unique.
The input file contains several game situations. Every test case starts with a line containing two integers w and h. These define width and height of the game rectangle, where 2 <= w, h <= 16.
Each of the next h lines contains a string of w characters. Each of these characters is either `x', `o' or `.', depending on the state of the corresponding square.
A blank line separates each game from the next. The input file ends with a game having w = 0 and h = 0. This game should not be processed.
For each test case you should first output a line containing the number of the game, followed by a line containing either `yes.' (if you can determine all `x' with at most one miss) or `no.' (if you cannot determine all `x' without at least two misses).
Output a blank line after every game.
10 10 .x..x..... oooooxoooo oxooxxx... xxoooooo.. xoooxooo.. ooxxxxoo.. oooooxxoox ooooooxoox ooooooooxx oooooooooo 0 0
Game #1 yes.
[End of Problem G]
| Source file: Input file: |
jury.pas/jury.c/jury.C jury.in |
In Frobnia, a far-away country, the verdicts in court trials are determined by a jury consisting of members of the general public. Every time a trial is set to begin, a jury has to be selected, which is done as follows. First, several people are drawn randomly from the public. For each person in this pool, defence and prosecution assign a grade from 0 to 20 indicating their preference for this person. 0 means total dislike, 20 on the other hand means that this person is considered ideally suited for the jury.
Based on the grades of the two parties, the judge selects the jury. In order to ensure a fair trial, the tendencies of the jury to favour either defence or prosecution should be as balanced as possible. The jury therefore has to be chosen in a way that is satisfactory to both parties.
We will now make this more precise: given a pool of n potential jurors and two values di (the defence's value) and pi (the prosecution's value) for each potential juror i, you are to select a jury of m persons. If J is a subset of {1,...,n} with m elements, then D(J) = sumk in J dk and P(J) = sumk in J pk are the total values of this jury for defence and prosecution.
For an optimal jury J, the value |D(J) - P(J)| must be minimal. If there are several jurys with minimal |D(J) - P(J)|, one which maximizes D(J) + P(J) should be selected since the jury should be as ideal as possible for both parties.
You are to write a program that implements this jury selection process and chooses an optimal jury given a set of candidates.
Note: If your solution is based on an inefficient algorithm, it may not execute in the allotted time.
The input file contains several jury selection rounds. Each round starts with a line containing two integers n and m. n is the number of candidates and m the number of jury members. These values will satisfy 1 <= n <= 200, 1 <= m <= 20 and of course m <= n. The following n lines contain the two integers piand di for i = 1,...,n. A blank line separates each round from the next.
The file ends with a round that has n = m = 0.
For each round output a line containing the number of the jury selection round (`Jury #1', `Jury #2', etc.).
On the next line print the values D(J) and P(J) of your jury as shown below and on another line print the numbers of the m chosen candidates in ascending order. Output a blank before each individual candidate number.
Output an empty line after each test case.
4 2 1 2 2 3 4 1 6 2 0 0
Jury #1 Best jury has value 6 for prosecution and value 4 for defence: 2 3
[End of Problem H]